
The goal here is to determine two things. First, how much of a rope can dangle off the edge of a table before it begins to slide? And second, once it does begin to slide, what is it's equation of motion? We will include friction, of course, otherwise the answer to the first question is a very boring "none of the rope!" However, we will simplify things to a certain amount, namely, we will ignore the effect of the edge of the table, and we will ignore any stiffness in the rope.
Andrew Paradis. Last edit: 2 January 2016
Alrighty. We have a piece of rope, and let's say it's total length is L. We dangle it over the edge of a table, and keep slightly tweaking it over until the rope finally starts to slide. We'll call the amount of rope dangling over the precipice x, because I'm feeling fancy and no one ever uses x as a variable. The situation is shown in the little sketch below.

We will account for the friction between the rope and table, and we need to recognize the two types of friction: static and kinetic. Static friction is commonly labeled \(\mu_s\), and represents the friction between things while they are not moving relative to each other. On the other hand, kinetic friction is commonly labeled \(\mu_k\), and represents the friction between things that are moving against each other. A frigidaire sitting on a loading ramp... static friction. A frigidaire, filled with laughing gnomes, sliding down the hills of San Francisco... kinetic friction.
Another thing we're going to assume is that the rope is more or less uniformly constructed. This is helpful, because it lets us describe its linear mass density, which is a fancy way of saying "mass per unit length." Because both "length" and "lambda" start with "L", we will use the Greek letter lambda to represent the linear mass density. It looks like this: \(\lambda\). Looks kind of like a very laid back person taking a very leisurely stroll.
Okay, enough exposition. Let's talk force. For things to remain in static equilibrium, meaning everything just stays put, then all the forces must cancel each other out. Considering our sketch, we can break it down into two areas: the table top, and the dangly bits.
On the table top, we have two forces at work: a tension in the rope, acting to pull the rope to the right, and the static frictional force, acting to keep us from going to the right (so it must act toward the left). We'll call the tension force \(T\) and the static frictional force \(f_s\). We'll take the positive direction as "to the right" and when we convert our description into math, we see that the sum of the table top forces are:
\[\sum {F_{table}}=T-f_s = 0 \]
Over the edge, we also have two forces at work: the same rope tension, acting to pull the rope up, and a gravitational force, acting to pull the rope down. We have already labeled the tension force (it's the same tension throughout the rope - any variations will be minimal), and we'll call the gravitational force \(W_x\), for "weight of x length of rope." Putting those together in math-land, and taking the positive direction as "down," we see that the sum of the dangly forces are:
\[\sum {F_{dangly}}=W_x-T = 0 \]
Like we mentioned before, we are in static equilibrium, so each batch of forces must cancel out (thank Newton for that). In other words, we can set our sums both equal to zero, and we get our force expressions:
\[T=f_s \]
\[W_x=T \]
Hold the phone! There is a \(T\) in each one of those last two equations! There is this cool rule in mathematics called the transitive law that states, more or less, "if two things are both equal to a third thing, then those two things are equal to each other." In other words, if \(A=B\) and \(B=C\), then \(A=C\). Looks like we've got ourselves a convoy! So, we can simplify things nicely and say:
\[W_x=f_s \tag{1} \]
Sweet. Now, let's get dangerous. The weight of the rope hanging over the edge depends on how much of it is hanging over the edge. And since weight in a gravitational field is found by \(W_x={mass}*g\), where \(g\) represents the strength of the gravitational field, then the weight of the dangly bit is:
\[W_x=x \lambda g = f_s \]
Notice we have replaced "mass" with the length of the dangling rope multiplied by the linear mass density (mass per unit length).
Now, the frictional force \(f_s\) is based on two things: the strength of static friction \(\mu_s\) between the rope and the table, and the weight of the rope laying on the table. Why? Think back to our gnome-filled frigidaire... if you added a lot more gnomes, it would make it harder to slide. If you try to slide a box over some gravel, then the heavier the box, the harder you have to push (because the frictional force is larger). We express this mathematically as:
\[f_s = \mu_s W_{table} = \mu_s (L-x) \lambda g \]
Notice again that we've replaced "mass" with our linear mass density shtuff, in this case the amount of rope laying on the table is \(L-x\), which we multiply by \(\lambda\) and \(g\).
From equation (1), we can equate our expressions to find:
\[x \lambda g = \mu_s (L-x) \lambda g \tag{2} \]
We can cancel out some stuff (\(\lambda g\)) and then rearrange a bit...
\[x = \mu_s (L-x) = \mu_s L - \mu_s x \Rightarrow x + \mu_s x = \mu_s L \]
And so we arrive at the length of rope that can dangle over the edge before things finally start to move:
\[x= \frac{\mu_s}{1+\mu_s}L \tag{3} \]
Now, let's set things in motion. We want to discover the equations of motion for the rope once we've passed the point of static equilibrium and it begins to slide off the table.
We can still use quite a bit from the earlier section, of course, but the differences are that instead of static friction, we are dealing with kinetic friction, \(\mu_k\), and the whole rope system is accelerating, and that can only mean one thing... Newton's Second Law!
Earlier, we were able to set various things to zero, using the argument that "they cancel out because we're in equilibrium." Well, no longer. Now that the system is accelerating, the sum of the forces isn't zero, but is proportional to the acceleration of the system.
Let's set some things up right at the start. The weight, \(W_{table}\) of the rope on the table is still \((L-x) \lambda g\), and the weight, \(W_x\) of the rope dangling over the edge is still \(x \lambda g\). This means that the frictional force, \(f_k\), resisting the sliding of the rope along the table is going to be:
\[f_k = \mu_k (L-x) \lambda g \]
So, for the part of the system that is on the table:
\[\sum {F_{table}} = T - f_k = T - \mu_k (L-x) \lambda g \tag{4a} \]
But, as previously discussed, this force sum is not zero, but is instead, by Newton's Second Law, equal to the mass multiplied by the acceleration.
\[\sum {F_{table}} = (L-x) \lambda a \tag{4b} \]
Did you notice that \(a\) doesn't have a subscript? Meaning, we don't have to talk separately about the "acceleration of the rope on the table" and the "acceleration of the rope over the edge" because they are the same thing. It's all the same rope. There is no spoon. The front, middle, and end of the rope are all moving at the same rate. That's handy. So, let's equate (4a) and (4b) and rearrange them to solve for the acceleration:
\[a(L-x) \lambda = T - \mu_k (L-x) \lambda g \tag{5} \]
Okay, looking good, looking peppy. But, problem. We don't know what \(T\) is. Fortunately, we still have the dangly bits to consider! Again, we're going to find a sum of forces, and again, we can't set it to zero. We'll use Newton's Second Law again, natürlich! So, for the part of the system that is dangling over the edge of the table:
\[\sum {F_{dangly}} = x \lambda g - T \tag{6a} \]
\[\sum {F_{dangly}} = x \lambda a \tag{6b} \]
Now let's equate (6a) and (6b), rearrange them a little, so that we can solve for \(T\).
\[T=x \lambda g - x \lambda a = x \lambda (g - a)\]
Sweet! Let's substitute this into equation (5) to get things just in terms of \(a\) and \(x\).
\[a(L-x) \lambda = x \lambda (g - a) - \mu_k (L-x) \lambda g\]
\[a(L-x) + a x = x g - \mu_k (L-x) g\]
\[a + \frac{x}{L-x} a = \frac{x}{L-x} g - \mu_k g\]
\[a \left ( \frac{L}{L-x} \right ) = \frac{x}{L-x} g - \mu_k g\]
\[a = \left ( \frac{g}{L} + \frac{\mu_k g}{L} \right ) x - \mu_k g\]
And we finally arrive at a tidy little solution for the acceleration of the system:
\[a = \frac{g(1+\mu_k)}{L} x - \mu_k g \tag{7} \]
So, although equation (7) is a perfectly fine solution, there is a bit of a practical problem. Notice that \(a \propto x\), yes? Well, \(x\) is continually changing, because the rope is sliding off the table! We'll want to do some stuff to this and come up with an equation of motion solely in terms of \(x\). And to pull that off, we'll need to hit some non-homogeneous linear second order differential equations (that's a mouthful!).
Before we jump into all that, let's simplify a bit. Let:
\[c = \frac{g(1+\mu_k)}{L}\]
\[k = \mu_k g\]
\[a = x''\]
The first two substitutions give us a simpler equation to work with, since the values used are all constants anyway, and at the end we can just put it all back together. The third one is just a restatement of "acceleration" as the second time derivative of position (sometimes that is written \(\frac{d^2 x}{dt^2}\), but it is simpler as just \(x''\). Our equation (7) then can be written:
\[x'' - cx - k = 0 \tag{8} \]
So, we want to find a function of \(x\) where it's second derivative cancels the original function... and friends, that sounds a LOT like an exponential!
As a quick reminder, if we have some function, \(y = e^{ax}\), then \(y' = ae^{ax}\) and \(y'' = a^2 e^{ax}\). See how the exponential keeps coming back, leaving just a few extra constant terms out front? To make it more obvious, just do a substitution:
\[y = e^{ax}\]
\[y'' = a^2 e^{ax} = a^2 y \]
\[y'' - a^2 y = 0 \]
With all that in mind, let's just guess a solution to equation (8). Hmmm... let's guess:
\[x = e^{rt}\]
We're using \(r\) as the constant just for convention's sake, and we're saying \(t\) is the variable, since the position will change over time. Now, if that's our solution, let's plug it in and see what would happen! Remember, it's just a guess, no one is going to die if we're wrong. If it doesn't work out, we'll just try something else. Oh, and for the moment we're just going to let \(k=0\) but we'll put it back soon. Doing this is called taking the complementary solution.
\[x = e^{rt}\]
\[x' = re^{rt}\]
\[x'' = r^2 e^{rt}\]
Now back into equation (8)...
\[r^2 e^{rt} - c e^{rt} = 0\]
\[e^{rt}(r^2 - c) = 0\]
Since exponentials can never really be zero (except at negative infinity, but we're being slightly realistic, here!), then the only way for the LHS to be zero is for \(r^2 = c\). This gives us two roots that we use to create the complementary solution, which we will label \(x_{comp}\). We also include a couple of constants, just to keep everything kosher... don't worry about them, we'll get their actual values in a bit; they're just place holders.
\[x_{comp} = A_1 e^{t \sqrt{c}} + A_2 e^{-t \sqrt{c}} \tag{9}\]
When solving differential equations of the sort we have, the general strategy is: 1) find a complementary solution, 2) find a particular solution, 3) combine them into the general solution. So, up in the last section we found the complementary solution by pretending \(k=0\). And we found it - it's equation (9), so hooray for us!
To find a particular solution, we make another guess. In this case, we want to guess something of the form of what we set to zero in the complementary solution. And since we know \(k\) is a constant, we will guess a constant solution for our particular solution. Yeah, I know, it sounds like freaking voodoo, but it all hinges on the idea that if you find any solution that works (by whatever means necessary, including guesswork), then you have found the actual solution to your problem!
Okay, so let's guess a particular solution that is a constant, \(x_{part} = B\). When we substitute this into equation (8), we see:
\[0 - cB = k \Rightarrow B = -\frac{k}{c} \]
And so we have our particular solution:
\[x_{part} = -\frac{k}{c} \tag{10} \]
There is another neat thing about these problems, and that is called the principle of superposition. Essentially, if you find two solutions to your problem, then adding those solutions together is another solution to the problem!
Our general solution, then, is just a linear combination of the complementary and particular solutions. So far, it still has a bunch of constants we need to solve for, but that is happening shortly. Therefore, the general solution, and it's first time derivative (we'll need it in a moment) are:
\[x = A_1 e^{t\sqrt{c}} + A_2 e^{-t\sqrt{c}} - \frac{k}{c} \tag{11a}\]
\[x' = A_1 \sqrt{c} e^{t\sqrt{c}} - A_2 \sqrt{c} e^{-t\sqrt{c}} \tag{11b}\]
Before we can make any more progress, we're going to need to discuss initial conditions. These are the "starting" points of our particular system. In our case, we have two initial conditions, because at the moment the rope begins to accelerate we know two things: 1) it's initial speed is zero (it starts from rest), and 2) it's initial value for \(x\) is given in equation (3) - it's the amount of rope hanging over the side just before it starts to slide. Mathematically, we write these conditions like this:
\[x(0) = \frac{\mu_s}{1+\mu_s}L \tag{12a} \]
\[x'(0) = 0 \tag{12b} \]
Remember, the variable is \(t\), for the elapsed time, and so \(x(0)\) means "the value of \(x\) when \(t=0\)." Well, that's just a simple substitution into our general solution and it's derivative shown in equations (11). We have:
\[\frac{\mu_s}{1+\mu_s}L = A_1 + A_2 - \frac{k}{c} \tag{13} \]
\[0 = A_1 \sqrt{c} - A_2 \sqrt{c} \Rightarrow A_1 = A_2 \]
Since \(A_1 = A_2\), we can just call them both \(A\). Then, using that in equation (13), we can solve for \(A\) in terms of our actual given constants from the problem. This nets us:
\[A = \frac{\mu_s}{1+\mu_s} \frac{L}{2} + \frac{k}{2c}\]
\[x = A \left ( e^{t\sqrt{c}} + e^{-t\sqrt{c}} \right ) - \frac{k}{c}\]
Now putting in all our constant values, we get a pretty darned fugly solution, but it's our solution, so we love it no matter what!
\[x = \left ( \frac{\mu_s L}{2(1+\mu_s)} + \frac{\mu_k L}{2(1+\mu_k)} \right ) \left ( e^{t \sqrt{\frac{g(1+\mu_k)}{L}}} + e^{-t \sqrt{\frac{g(1+\mu_k)}{L}}} \right ) - \frac{\mu_k L}{1+\mu_k} \tag{14} \]
Can we neaten this up a bit? Well, let's consider the "pretty good" approximation of \(\mu_s = \mu_k\)... this isn't terribly far-fetched, as the ranges given in the engineering literature for these values have a LOT of cross-over! Each of them have values varying from 0.4 to 0.7. We also want to clean up the bulky square root signs, so we should make arrangements there as well. So, let's just say that:
\[\mu_k = \mu_s = \mu\]
\[D = \sqrt{\frac{g(1+\mu)}{L}}\]
Using these simplifications, we can get a better feel for what our general solution "is," no matter what your definition of "is" is.
\[x = \frac{\mu L}{1+\mu} \left ( e^{tD} + e^{-tD} -1 \right )\]
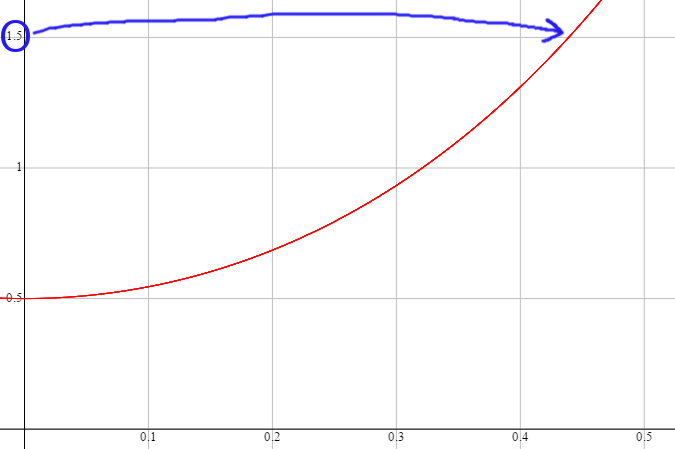
Using a few reasonable values, \(\mu = 0.5\) and \(L = 1.5\)m, we find that \(D \approx 3\), and that \(\frac{\mu L}{1+\mu} = \frac{1}{2}\).
\[x = \frac{1}{2} \left ( e^{3t} + e^{-3t} - 1 \right )\]
This equation has a cute little graph, shown below. An important thing happens at around \(t=0.45\) seconds... the rope falls off the table!
And that's a reasonable enough place to leave things!